細胞システム動態の分岐解析と疾患制御への応用
 研究代表者
研究代表者
田中剛平
東京大学 工学系研究科
http://www.sat.t.u-tokyo.ac.jp/~gouhei/
研究概要
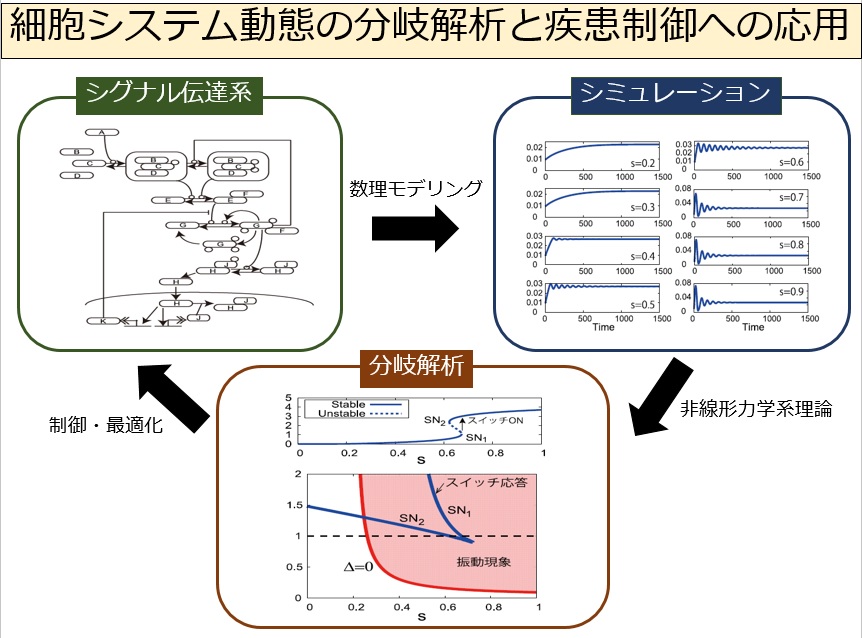
生体内のシグナル伝達は、多数の因子や反応が関係する複雑なシステムである。因子間の相互作用関係はしばしばフィードバックループを含む複雑なネットワークを構成し、個々の反応も非線形であるため、要素還元論的アプローチによって全体の仕組みを理解することが困難な場合が多い。正常な生体機能がどのように維持されているのか、またそれがどのようなきっかけによって破綻するのかを体系的に理解するための一つの方法は、システム科学のアプローチである。システム生物学では、シグナル伝達系を刺激入力に対して動的な応答出力を与える「システム」と見なし、細胞応答のダイナミクスを理解することを目指す。近年では、様々な実験データを再現する詳細なシグナル伝達系の数理モデルが構築されてきているが、それらはしばしば高次元非線形力学系であるためモデル解析が容易ではなく、モデルの性質を体系的に理解するための数理解析技術・理論の開発が求められている。
本研究では、細胞システムの数理モデルが示す非線形現象を力学系の分岐理論の観点から解析し、細胞ダイナミクスにとって本質的な機構および重要因子を特定するための数理的技術の発展を目指す。特に、外部刺激入力や重要因子の濃度レベルが変化したときに細胞応答が劇的に変化する定性的変化に着目し、それを理解するための分岐解析手法の開発を重点的に行う。私達はこれまでに、NF-kBシグナル伝達系のコアモデル(低次元モデル)を対象とし、振動現象とスイッチ応答現象の解析を行ってきた。しかし、低次元モデルが元の高次元モデルのダイナミクスを十分に反映しているかは、不明である。そこで、本研究では、NF-kBシグナル伝達系の高次元モデルを対象として、分岐解析技術の発展を目指す。
また、アレルギー疾患の数理モデルを対象として、疾患を発症する条件を分岐現象の観点から特定し、それを制御するための有効な治療方法について検討する。治療オプションをモデルに取り入れ、薬剤の量や投与プロトコルの治療効果を明らかにする。最終的には、モデルから示唆されたより良い治療オプションを実験研究者にフィードバックし、実験による検証につなげたい。
参考文献
- 田中 剛平, 細胞システムの動態と分岐理論, 生物物理, vol. 56, no. 6, pp. 340-344 (2016).
- K. Inoue, H. Shinohara, M. Behar, N. Yumoto, G. Tanaka, A. Hoffmann, K. Aihara, and M. Okada-Hatakeyama, “Oscillation Dynamics Underlie Functional Switching of NF-kB for B Cell Activation,” npj Systems Biology and Applications, vol. 2, article no. 16024 (2016).
- G. Tanaka, K. Morino, and K. Aihara, “Dynamical Robustness of Complex Biological Networks,” In: (Eds) T. Ohira and T. Uzawa, Mathematical Approaches to Biological Systems: Networks, Oscillations, and Collective Motions, Springer, Chapter 2, pp. 29-53 (2015).
- B.-G. Zhang, G. Tanaka, K. Aihara, M. Honda, S. Kaneko, and L. Chen, “Dynamics of an HBV model with drug resistance under intermittent antiviral therapy,” International Journal of Bifurcation and Chaos, vol. 25, no. 7, 1540011 (2015).
- G. Tanaka and K. Aihara, “Effects of Seasonal Variation Patterns on Recurrent Outbreaks in Epidemic Models,” Journal of Theoretical Biology, vol. 317, pp. 87-95 (2013).
- G. Tanaka, K. Morino, and K. Aihara, “Dynamical robustness in complex networks: the crucial role of low-degree nodes,” Scientific Reports, vol. 2, 232 (2012).
- G. Tanaka, Y. Hirata, N. Bruchovsky, S. Goldenberg, and K. Aihara, “Mathematical Modelling of Prostate Cancer Growth and its Application to Hormone Therapy,” Philosophical Transactions of the Royal Society A, vol. 368, pp. 5029-5044 (2010).
- G. Tanaka, K. Tsumoto, S. Tsuji, and K. Aihara, “Bifurcation Analysis on a Hybrid Systems Model of Intermittent Hormonal Therapy for Prostate Cancer,” Physica D, vol. 237, pp. 2616-2627 (2008).
- A. Ideta, G. Tanaka, T. Takeuchi, and K. Aihara, “A Mathematical Model of Intermittent Androgen Suppression for Prostate Cancer,” Journal of Nonlinear Science, vol. 18, no. 6, pp. 593-614 (2008).








